DFT & RDMFT Development
The group works on density (DFT) and density-matrix functional theories (DMFT). DMFT is also known as reduced density matrix functional theory, RDMFT, or when the approximations are based on natural orbitals, natural orbital functional theory, NOFT.
DFT being the workhorse of computational calculations, we have focused most of our late efforts into analyzing density functional approximations (DFA) and their limitations. We have identified a number of challenges in the computation of molecular properties, several of which were entirely unprecedented in the literature. For example, we recently discovered that the accuracy of vibrational corrections to nonlinear optical properties (NLOPs) and to many vibrational spectroscopic quantities (e.g., harmonic and anharmonic IR and Raman frequencies and intensities) shows a critical dependence on the numerical integration grid —an issue that had previously gone unnoticed in density functional approximations [1,2]. In some cases, extremely poor results are obtained even when using prohibitively large grids, leading to the alarming conclusion that certain popular DFAs, such as M06-2X or ωB97X-D, are completely unreliable for computing vibrational spectroscopic quantities [1-4].

This limitation hinders the simulation of high-precision spectra, such as those required for species identification in the interstellar medium or for studying atmospheric chemistry reactivity. We have also found that the delocalization error (DE) leads to a systematic overestimation of electron delocalization and aromaticity [5-7] compromising the description of large nanorings [8,9]. Altogether, these findings underscore the need for a careful and systematic examination of electronic-structure methods when exploring molecular properties. Our group has worked in the design of new density functional approximations [10-12].
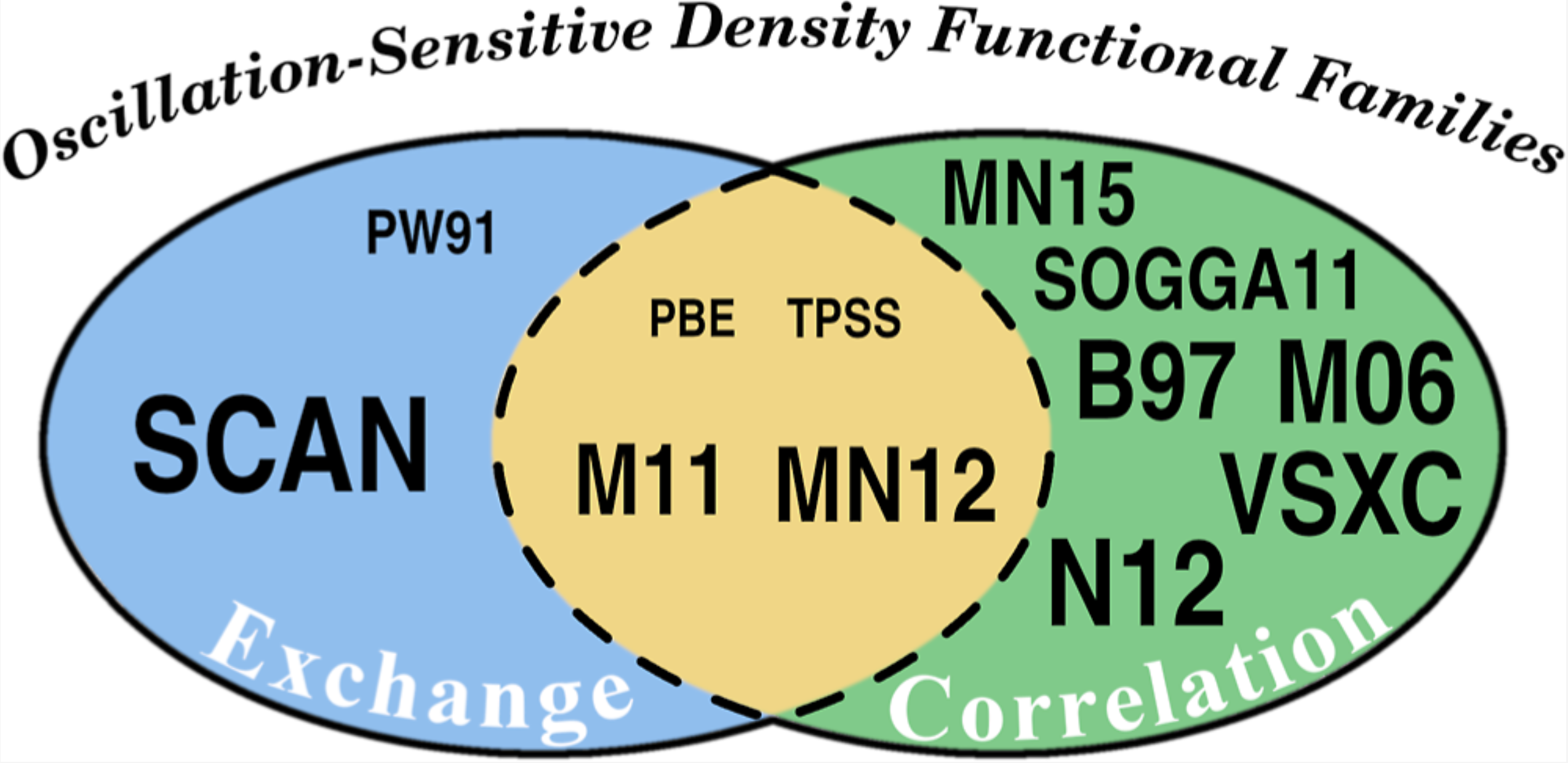
Our efforts in RMDFT have concentrated on the analysis of approximations [13-15] and benchmarking studies [14-16], from where we have obtained value knowledge about the limitation of current NOFT approximations. In particular, we have identified to valuable constraints for the cumulant matrix [17], which are currently employed to improve some NOFT approximations [18].
Recent publications:
1. Zaleśny R.; Medved’ M.; Sitkiewicz S. P.; Matito E.; Luis J. M.; Can density functional theory be trusted for high-order electric properties? The case of hydrogen-bonded complexes. J. Chem. Theory Comput. 15, 3570–3579 (2019).
2. Sitkiewicz S. P.; Zaleśny R.; Ramos-Cordoba E.; Luis J. M.; Matito E.; How reliable are modern density functional approximations to simulate vibrational spectroscopies? J. Phys. Chem. Lett. 13, 5963–5968 (2022).
3. Sitkiewicz S. P.; Matito E.; Luis J. M.; Zaleśny R.; Pitfall in simulations of vibronic TD-DFT spectra: Diagnosis and assessment. Phys. Chem. Chem. Phys. 25, 30193–30197 (2023).
4. Sitkiewicz S. P.; Ferradás R. R.; Ramos-Cordoba E.; Zaleśny R.; Matito E.; Luis J. M.; Spurious Oscillations Caused by Density Functional Approximations: Who is to Blame? Exchange or Correlation? J. Chem. Theory Comput. 20, 3144–3153 (2024).
5. Casademont-Reig I.; Woller T.; Contreras-García J.; Alonso M.; Torrent-Sucarrat M.; Matito E.; New electron delocalization tools to describe the aromaticity in porphyrinoids. Phys. Chem. Chem. Phys. 20, 2787–2796 (2018).
6. Casademont-Reig I.; Ramos-Cordoba E.; Torrent-Sucarrat M.; Matito E.; How do the Hückel and Baird Rules Fade away in Annulenes? Molecules 25, 711 (2020).
7. Casademont-Reig I.; Woller T.; García V.; Contreras-García J.; Tiznado W.; Torrent-Sucarrat M.; Matito E.; Alonso M.; Quest for the Most Aromatic Pathway in Charged Expanded Porphyrins. Chem. Eur. J. 29, e202202264 (2023).
8. Casademont-Reig I.; Guerrero-Avilés R.; Ramos-Cordoba E.; Torrent-Sucarrat M.; Matito E.; How Aromatic Are Molecular Nanorings? The Case of a Six-Porphyrin Nanoring. Angew. Chem. Int. Ed. 60, 24080–24088 (2021).
9. Casademont-Reig I.; Soriano-Agueda L.; Ramos-Cordoba E.; Torrent-Sucarrat M.; Matito E.; Reply to the Correspondence on “How Aromatic Are Molecular Nanorings? The Case of a Six-Porphyrin Nanoring”. Angew. Chem. Int. Ed. 61, e202206836 (2022).
10. Matito E., Casanova D., Lopez X., Ugalde J.M.; Exact Exchange Functional for the Stretched Hydrogen Molecule. Theor. Chem. Acc. 135, 226 (2016)
11. Besalú-Sala P., Sitkiewicz S.P., Salvador P., Matito E., Luis J.M.; New Optimally-Tuned Range-Separation Density Functional for the Accurate Calculation of Electronic Second Hyperpolarizabilities. Phys. Chem. Chem. Phys. 22, 11871 (2020)
12. Paulau A., Salvador P., Luis J.M., Ramos-Cordoba E., Matito E., in preparation.
13. Ramos-Cordoba E., Lopez X., Piris M., Matito E.; H4: A Challenging System For Natural Orbital Functional Approximations. J. Chem. Phys. 143, 164112 (2015)
14. Cioslowski J., Piris M., Matito E.; Robust Validation of Approximate 1-Matrix Functionals With Few-Electron Harmonium Atoms. J. Chem. Phys. 143, 214101 (2015)
15. Rodriguez-Mayorga M., Ramos-Cordoba E., Via-Nadal M., Piris M., Matito E.; Comprehensive Benchmarking of Natural Orbital Functional Approximations. Phys. Chem. Chem. Phys. 19, 24029 (2017)
16. Via-Nadal, et al., unpublished.
17. Ramos-Cordoba E.; Salvador P.; Piris M.; Matito E.; Two New Constraints for the Cumulant Matrix. J. Chem. Phys. 141, 234101 (2014).
18. Chuiko V., Ayers P.W., Matito E., under preparation.
