Electron Correlation
The reliability of predictions in computational chemistry rests on the ability of computational methods to capture electronic correlation accurately at a reasonable computational cost [1-10]. The concept of electronic correlation arises from the approximate nature of the fundamental Hartree–Fock (HF) method which, despite its generally good performance, underestimates electron–electron interactions and therefore provides a poor description of many chemical phenomena.
Electronic correlation is commonly classified into dynamic and non-dynamic correlation. While dynamic correlation is a universal effect and its inclusion is mandatory for an accurate description of chemical systems, it is often reasonably well captured within dispersion-corrected Kohn–Sham Density Functional Theory (KS-DFT). In contrast, non-dynamic correlation is poorly described by KS-DFT and other single-reference methods, requiring the use of multireference (MR) approaches such as Complete Active Space Self-Consistent Field (CASSCF), multireference configuration interaction, or the density matrix renormalization group.
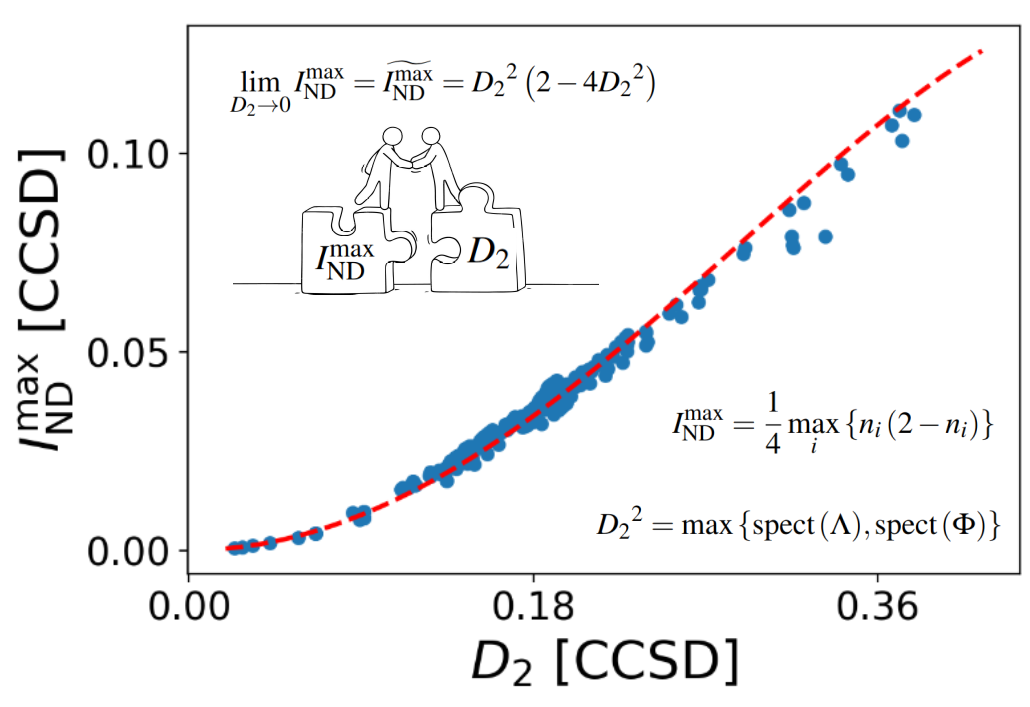
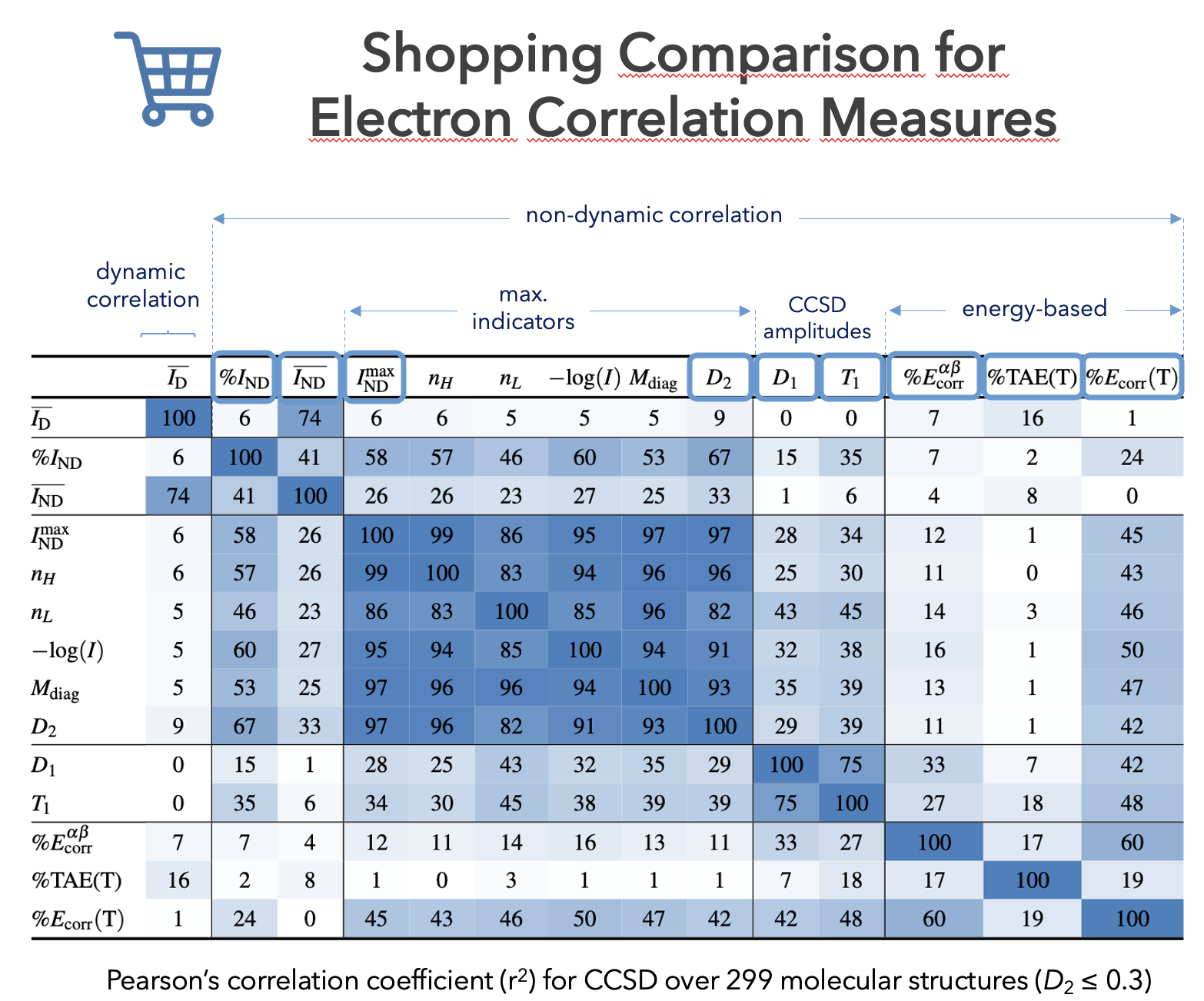
Machine-learning models are typically trained on large datasets generated using KS-DFT. This requires high-throughput screening to identify and exclude molecules that require MR treatments, since their inclusion may contaminate the dataset and compromise the training process. Therefore, the development of correlation diagnostics capable of identifying MR systems is essential. Such diagnostics are valuable not only for high-throughput screening, but also for individual molecular studies, where accurate simulations depend on the choice of an appropriate computational method.
Over the past years, our research activity has focused primarily on the study of electronic correlation and on the development of new computational methods. Our group has developed both scalar [3,10] and local [2,9] descriptors that enable the separation of dynamic and non-dynamic correlation [5]. These indicators have been employed in the design of new wave-function-based electronic structure methods, such as spin-component-scaled perturbation methods and hybrid approaches [1]. In addition, we have developed a range-separated partitioning of the pair density [4-5], which allows for the identification of the type of correlation present in a molecule and can be used in the design of range-separated hybrid electronic structure methods, as well the identification of dispersion interactions [5,7].
References:
1. Paulau A., Soriano-Agueda L., Matito E.; Correlation-driven spin-component-scaled second-order Møller-Plesset perturbation theory (CD-SCS-MP2). J. Chem. Theory Comput. 21, 9601 (2025)
2. Xu X., Soriano-Agueda L., López X., Ramos-Cordoba E., Matito E.; How Many Distinct and Reliable Multireference Diagnostics Are There? J. Chem. Phys. 162, 124102 (2025)
3. Xu X., Soriano-Agueda L., Lopez X., Ramos-Cordoba E., Matito E.; An All-Purpose Measure of Electron Correlation for Multireference Diagnostics. J. Chem. Theory Comput. 20, 721 (2024)
4. Via-Nadal M., Rodríguez-Mayorga M., Ramos-Cordoba E., Matito E.; Natural Range Separation of the Coulomb Hole. J. Chem. Phys. 156, 184106 (2022)
5. Via-Nadal M., Rodríguez-Mayorga M., Ramos-Cordoba E., Matito E.; Singling Out Dynamic and Nondynamic Correlation. J. Phys. Chem. Lett. 10, 4032 (2019)
6. Rodríguez-Mayorga M., Ramos-Cordoba E., Lopez X., Solà M., Ugalde J. M., Matito E.; The Coulomb Hole of the Ne Atom. ChemistryOpen 8, 411 (2019)
7. Via-Nadal M., Rodriguez-Mayorga M., Matito E.; Salient Signature of van der Waals interactions. Phys. Rev. A rapid comm. 96, 050501 (R) (2017)
8. Rodriguez-Mayorga M., Ramos-Cordoba E., Feixas F., Matito E.; Electron Correlation Effects in Third-Order Densities. Phys. Chem. Chem. Phys. 19, 4522 (2017)
9. Ramos-Cordoba E., Matito E.; Local Descriptors of Dynamic and Nondynamic Correlation. J. Chem. Theory Comput. 13, 2705 (2017)
10. Ramos-Cordoba E., Salvador P., Matito E.; Separation of Dynamic and Nondynamic Correlation. Phys. Chem. Chem. Phys. 18, 24015 (2016)
